Calculating the Fall of a Dynasty:
Divination Based on the Qian zuo du
Bent Nielsen
(Department of Cross-Cultural and Regional Studies, Chinese Section, University of Copenhagen, Denmark)
Introduction
The Qian zuo du乾凿度 dates to the middle centuries of the Han dynasty (202 BCE–220 CE) and is one of the earliest surviving studies of the Book of Changes (Yijing易经). The title may be rendered into English as “chiseling through to the regular system of the hexagram Qian”. The hexagram Qian乾 is, of course, the first of the 64 hexagrams constituting the core of the Book of Changes. Among other things, it symbolizes the yang阳 force and heaven. So the title should probably be understood along the lines of “revealing the activities and intentions of heaven”.
From at least the 6th century the Qian zuo du乾凿度 (hereafter QZD) was included in a corpus known as the Wei shu纬书, which in the west is commonly translated as ‘apocrypha'. The term Wei shu纬书 seems to have been but one of many designations for a certain kind of prognostication texts emerging during the 1st century CE. These texts served a political purpose, and many instances of both political application and political repression are on record, which explains why only a handful of these texts has survived as more than fragments.
The authors of the Wei shu纬书 are anonymous; the texts were attributed to sage kings and other legendary figures of the past. The author of the QZD uses the name of Confucius to voice his ideas and advocates humanity and righteousness (ren仁 and yi义). His preoccupation with yin阴 and yang阳 and the five phases (wu xing五行) may classify him as a typical Han Confucian, an intellectual descendant of Dong Zhongshu董仲舒 (2nd cent. BCE), and his erudition in the Book of Changes certainly grants him scholarly kinship with such renowned experts as Jing Fang京房 and Meng Xi孟喜 (both 1st cent. BCE). The latter are associated with the New Text edition of the Book of Changes and their particular schools or traditions—with which the author of the QZD clearly is acquainted—came to be known from the Song dynasty (960-1279) on as those of images and numbers (xiang shu象数). The author's intimate familiarity with numerology, magic squares, and calendar computations also indicates an affinity with a rather loosely defined group of intellectuals generally known as fang shi方士, in a somewhat anachronistic term, masters of know-how. In fact, he fits very well the description of a certain Fan Ying樊英 of whom it is said, he was skilled in Jing Fang's京房 comments on the Book of Changes, well-read in the Five Classics, and an adept in Stellar Calculations, Yellow River charts, Luo River scripts, the seven Apocrypha, and interpretations of disasters and disorder.
As is well-known, natural disasters and cosmic disorder played an immensely important role in politics during the Han dynasty, and the need for correct interpretations of these phenomena was correspondingly acute. Omens and portents were feared political tools used by contending factions at court, and beginning with the History of the Han (Han shu汉书) complete chapters—the so-called Treatises of the Five Phases (Wu xing zhi五行志)—of the dynastic histories are devoted to this subject. The rationale behind these assumptions was the belief in a cosmic resonance between heaven, earth, and man, and by the 1st century CE this trinity and the cycles of yin and yang and the five phases had formed the backdrop of a revival and reinterpretation of the ancient Chinese concept of the mandate of heaven (tian ming天命), the right to exercise power.
The examination system, which had been steadily expanded and improved upon since its establishment around 130 BCE, meant that there was a large educated class sharing the same ideas and the same frame of reference. They could be trusted to understand allusions in a cosmological context and to react accordingly. As the political situation became increasingly unstable towards the end of the 1st century BCE, portents and prognostications became of greater significance. The ruling house was gradually losing the initiative to the Wang family which had supplied the imperial consort of emperor Yuan元帝 (r. 48-33 BCE). During the reign of emperor Cheng 成帝(33-7 BCE) members of the Wang family succeeded each other as de facto heads of state, and the decline of the Han culminated in Wang Mang's王莽 assumption of the imperial title and foundation of the Xin Dynasty in 9 CE.
Wang Mang's claim to the mandate of heaven depended upon an overwhelming deployment of omens and portents linked with the cycles of the five phases and the alternation of yin and yang. A combination of dissatisfaction among the nobility and general unrest—known as the rebellion of the Red Eyebrows—following a flooding of the Yellow River caused the downfall of Wang Mang and his dynasty in 23 CE.
When the Han dynasty was restored to power in 25 CE, it was in reliance on the mandate of heaven, the five phases etc., that emperor Guangwu光武 (r. 25-57) claimed authority, and politics during the reigns of the Han emperors of the 1st century CE were dominated by these theories. As opposed to Wang Mang who chiefly availed himself of various natural phenomena, Guangwu relied heavily on prognostication texts.
Such was the political and intellectual climate the author of the QZD found himself in. While some official scholars searched other classics for hidden references to divine kingship in support of one faction or another, the Book of Changes—the core of which is an ancient divination manual—naturally presented itself to those who wished to look into the future. Some time during the 3rd century BCE anonymous philosophers attempted to build a cosmology around this divination manual and some of their writings are now included in the Book of Changes. These texts were not only known to the author of the QZD, they constitute the basis of his philosophy. During the reigns of emperor Guangwu光武 and his successors all kinds of prognostication texts and charts were consulted but those experts who possessed knowledge of calendar related methods of divination probably carried more weight as they were drawing on an ancient established tradition. From the camp of sceptical scholars that gradually formed during the Later Han period, criticism was leveled against various ways of obtaining knowledge of the future but the Book of Changes seems to have been largely above reproach. For example, the notable sceptic Zhang Heng张衡(78-139) voiced his critique against false and empty prophecy-making, while maintaining that predictions based on the way of heaven as known by means of the Book of Changes and the calendar are perfectly valid.
Calendar making was an imperial prerogative which served both practical and symbolic purposes. The importance attached to an accurate calendar by the ruling house cannot be exaggerated, but mostly when a new calendar was introduced, it was rarely for practical purposes. The main concern of the court astronomers was the calendar's capability to predict eclipses so it could be demonstrated that the emperor was in agreement with the celestial cycles. Several times during the Han dynasty new calendars were introduced (twice in the 1st century CE) and they were primarily adopted as a symbolic act accompanying the accession of a new emperor, the inauguration of a new reign period or to reconfirm possession of the Mandate.
A crucial issue during the 1st century was: Could the mandate of heaven be exhausted? Whereas the mandate of heaven as it was applied to the early Zhou kings a thousand years earlier was meant to legitimize their conquest, the mandate of heaven during the Han had become linked with the future of the ruling house, the destiny of the dynasty. Precisely because it was combined with and followed the cycles of the five phases, it was acknowledged that the mandate of heaven could not last forever. If a family rules under the protection or by virtue of one of the five phases, for example, that symbolized by fire, this phase will sooner or later be replaced by the next, which may be water according to one of several prevalent theories. From memorials submitted in the late 1st century BCE, it is clear that certain circles entertained the idea that the house of Han had exhausted its mandate to rule. It is equally clear, however, that this did not necessarily mean the fall of the house of Han because it was possible to renew the mandate by adopting the required measures. These measures are not spelled out but such a reinstatement of the ruling house would probably involve the changing of reign title, maybe a change of and adaptation to the symbolic values of the next phase, possibly the introduction of a new calendar etc.
However, partisans of the Han insisted that the ruling family had received heaven's eternal mandate (tian yong ming天永命), which, if nothing else, emphasizes the general belief in the transient nature of the mandate. It seems that the author of the QZD composed his work with the express purpose of correlating the hexagrams of the Book of Changes with the calendars known in the early 1st century CE in order to be able to calculate the duration of the dynasty and lend support to emperor Guangwu's光武 accession. As many historians of the Han dynasty has shown, the cosmological theories developed rapidly during the 2nd and 1st centuries BCE, so it was of great urgency to the author, who almost exclusively relies on the Book of Changes, to demonstrate that the by then somewhat naive cosmology in this classic could still apply when correctly understood.
Judging from the present edition of the QZD, the authors immediate concern was to define yi易, the term for change, which is also the title of the Book of Changes, to trace the origins of the hexagrams as well as how they relate to numbers, and to establish a rationale for the sequence in which they occur in the Book of Changes. This sequence is of great importance when the hexagrams are correlated to the calendar. Finally, he expands the idea of the magic squares (the so-called river diagrams) to include additional spatial and temporal concepts as well as to incorporate traditional Confucian moral philosophy.
Allowing for certain textual difficulties, the contents of the first of the two chapters are presented in a logical and systematic way which guides the reader through to the main point: The correlation between the hexagrams and the calendar. As the present edition of the QZD is compiled from an encyclopedia this presentation probably reflects the efforts of a later editor.
The compilers of the calendar treatises in the History of the Later Han (Hou Han shu后汉书) refer to the QZD as an authoritative text on which calendar computations could be based. During the 1st century CE the Wei shu纬书 had an important impact on calendar reforms; an impact which had both positive and negative consequences so far as the precision with which eclipses could be predicted was concerned. However, in the last analysis the calendar calculators tried to steer away from the influence of the Wei shu纬书, and by the end of the 1st century, astronomers had ceased using the Year Star (Sui xing岁星)—the invisible counter-rotating correlate to Jupiter—to record the years. The abandonment of this method paved the way for more accurate predictions of eclipses and the separation of the calendar and the Wei shu纬书. For example, the calendar used in the kingdom of Shu蜀 in the 3rd century was entirely free of the numerology of the Wei shu纬书.
Calendar Calculations and Numerology
Much of the numerology associated with the Book of Changes is related to calendar computations. An obvious example occurs in the paragraph on the Great Expansion (Da yan大衍) in the Commentary on the Attached Words (Xi ci zhuan系辞传) of the Ten Wings (Shi yi十翼) where the milfoil sticks used for divination are said to correspond to the days of the year. It is generally agreed that this paragraph, which has come down to us in two slightly different redactions, is the earliest known attempt to describe the divination method with milfoil sticks. The older of the two redactions is that of Kong Yingda's孔颖达(574-648) Correct Meaning of the Zhou Changes (Zhou yi zheng yi周易正义), which is traceable back through Wang Bi王弼 (226-249) to the old text edition of Fei Zhi费直 (c. 50 BCE–10 CE). Here the paragraph constitutes section 8 of the 1st part:
The number of the Great Expansion is 50; those used are 49. [These 49] are divided into 2 to represent 2. Suspend 1 in order to represent 3. Draw them (i.e. the divination sticks) by [groups of] 4 to represent the 4 seasons. Go back to the remainder [and place this in] the space between the fingers in order to represent the intercalations. In 5 years there are two intercalations, therefore twice [return the remainder to] the space between the fingers and afterwards suspend [these; i.e. the sticks placed between the fingers]. Heaven's numbers are five, earth's numbers are five. The five positions having obtained one another, each has a match. Heaven's numbers [total] 25, earth's numbers [total] 30. Both heaven's and earth's numbers [total] 55. This is that which having completed the alternations and transformations, sets in motions the gui- and the shen-spirits. Qian's divination sticks are 216, and Kun's divination sticks are 144. The total is 360 corresponding to the days of a year. The divination sticks of the two chapters [of the Zhou yi] are 11,520 corresponding to the number of the myriad things. Therefore, having four steps completes the Changes, and having eighteen alternations complete the hexagrams. Having eight trigrams, there is a small completion. By stretching and extending them, stirring the categories and increasing them, the possible matters of the world are concluded. This displays the Way and the spirits and virtuous conduct. Therefore, we can pledge with wine and we can entertain the spirits.
In Zhu Xi's 朱熹(1130-1200) Original Meaning of the Zhou Changes (Zhou yi ben yi周易本义) this paragraph occurs as section 9 part 1 of the Commentary on the Attached Words, which is rearranged and divided into two parts of 12 sections each instead of Kong Yingda's孔颖达 two parts of 12 and 9 sections, respectively (throughout this paper my references are to Kong Yingda's edition). Zhu Xi based his reorganization on Cheng Yi's程颐(1033-1107) and Lü Zuqian's吕祖谦(1137-1181) arrangements of the text. In addition to that, he may have based himself on a quotation from the Commentary on the Attached Words in the History of the Han, which indicates that the first 64 characters of section 9 of Zhu Xi's edition belong together. These characters occur in two different sections in Kong Yingda's孔颖达edition. Zhu Xi's朱熹 reconstruction is as follows (ellipsis points indicate where Kong Yingda's section 8 quoted above occurs):
Heaven is one, earth is two. Heaven is three, earth is four. Heaven is five, earth is six. Heaven is seven, earth is eight. Heaven is nine, earth is ten. Heaven's numbers are five, earth's numbers are five. The five positions having obtained one another, each has a match. Heaven's numbers [total] 25, earth's numbers [total] 30. Both heaven's and earth's numbers [total] 55. This is that which having completed the alternations and transformations, sets in motions the gui- and the shen-spirits. […] The Master said, “He who knows the way of alternation and transformation, does he not also know the doings of the spirits!”
During the formative stages of hexagram divination, the numerology was in all probability developed from temporal concepts. In fact, this may have been the case from the very beginning as suggested by Qu Wanli屈万里(1907-79) by advancing the theory that the six lines of the hexagrams are based on the Shang dynasty's 10-day weeks of which there were six within the so-called sexagenary cycle of the stems and branches. Other obvious examples are the number of Qian's and Kun's divination sticks, which total 360 corresponding to the days of a lunar year, the 384 lines of the 64 hexagrams, which correspond to the number of days in a year with an intercalary month, and the numerical designations 6, 7, 8, and 9, which result in 30 when added. These are clear examples of conscious correlations with a relatively primitive calendar.
Thus, the numerology of the Book of Changes is at least partly based on early calendrical calculations, which contributed to its reputation both as a manual of divination and as a cosmological text. During the Han dynasty this reputation, in turn, had a strong influence on the calendar calculators who could not avoid the entanglements of this numerology, especially as this was propounded by the authors of the apocrypha. This is attested by the numerous quotations from and references to the Book of Changes in the chapters on pitch-pipes and the calendar (Lü li律历) of the History of the Han and the History of the Later Han, as well as references to the apocrypha in the latter. Jack Dull sums up the role of the apocrypha as a two-edged sword: “The apocryphal literature was an important factor in the one major calendrical reform of the Later Han dynasty and it was also in part responsible for preventing further reforms and thereby preserving an inefficient and outdated calendar.”
Several pages in the History of the Later Han are devoted to the problems arising when trying to integrate the numerology of, among others, the QZD into calendrical calculations. In Mansvelt Beck's opinion, because “they carried the authority of antiquity, it was necessary that the calendar be adapted to the theories developed in the Diagrams and Apocrypha,” but he also observes, “that in the last analysis the calendar calculators try to steer away from the influence of these books.”
The Han calendars that are relevant for this discussion are the Calendar of the Great Beginning (Tai chu li太初历), the Three Concordances Calendar (San tong li三统历), and the Quarter Remainder Calendar (Sifen li四分历). The Calendar of the Great Beginning is the earliest calendar system, which is known in some detail. Devised by Luoxia Hong落下闳(fl. c. 140-87 BCE) and Deng Ping邓平 (fl. c. 104 BCE) among others, it was based on a year of 365 1/4 days. The Calendar of the Great Beginning was used from 104 BCE until it was superseded by the Three Concordances Calendar, which represents the improvements made by Liu Xiang刘向 (79-8 BCE) and Liu Xin刘歆 (46 BCE–23 CE). It has been debated to what extent Liu Xin merely copied the methods and constants of the Calendar of the Great Beginning, but in Nathan Sivin's opinion, Liu Xin also “with great originality extended them (i.e. the methods and constants) into a universal system which became the pattern for his successors.” The Three Concordances Calendar was probably inaugurated in 6 CE and remained in use until it was superseded by the Quarter Remainder Calendar in 85 CE. The ‘three concordances' refer to the three periods, which constitute a period of resonance in this system, i.e. one of “those rather longer lapses of time which end in approximate concordance of phase.” Sivin explains a resonance period as follows:
Cycles were determined for the phenomena to be represented, and, by a process which amounts to finding lowest common multiples, larger cycles were constructed to contain and subsume series of smaller ones. This system was made integral, when this process was done, by a “great year” cycle, like an immense wheel driving a congeries of graduated smaller wheels arranged in subsystems. It was then necessary to find the epoch, to determine just how long ago the largest cycle had begun. Then the state of any of the smaller cycles, which by definition began at the same time, could be determined ...
For example, 19 tropical years are approximately of the same length as 235 lunations, and this is the shortest period of time within which any constellation of the sun and the moon will return on the same day. A cycle of 19 years or 6,939 3/4 days is called a Rule Cycle (zhang章), and four such cycles correspond to what the QZD refers to as the Era Cycle. Twenty Era Cycles are called the Obscuration Cycle (bushou蔀首), and three of these constitute the Epoch Cycle (yuan元), which is equivalent to 4,560 years and may be considered a ‘great year' cycle or a resonance period. These cycles belong to the Quarter Remainder Calendar, but in the Three Concordances Calendar the resonance period is also known as the Epoch Cycle (yuan), only here it is 57 years longer, i.e. 4,617 years. This Epoch Cycle comprises three Concordance Cycles (tong统) of 1,539 years each.
The Han astronomers were able to calculate the length of a month and a year with great precision. The Quarter Remainder Calendar, which is slightly more accurate than the Three Concordances Calendar, deviates from the modern figures of the tropical year by a mere 0.00781 day and the synodic month by only 0.0002631 day. The History of the Han has a perfect example of the relationship between the numerology of the Book of Changes as expressed in the Ten Wings and the apocrypha on the one hand, and the calendar calculations as these are expounded in the chapters on the pitch-pipes and calendars on the other:
Therefore, for the Primordial Beginning there is the representation of one, for the Springs and Autumns there are two, for the Three Sequences there are three, and for the four seasons there are four. Combined they are ten and complete the five [heavenly] bodies. Multiplying five by ten [results in] the number of the Great Expansion, but the Way takes one of them. The remaining 49 are those that should be used, so in divination with plant sticks this is considered the [correct] number. To represent two this is doubled (49 x 2 = 98). Furthermore, to represent three this is tripled (98 x 3 = 294). Furthermore, to represent four it is quadrupled (294 x 4 = 1,176). Also, go back to the remainder representing the intercalary 19 and the one that was taken and add these (1,176 + 19 + 1 = 1,196). Because [the sticks are] twice [placed in] the space between the fingers, it is doubled (1,196 x 2 = 2,392). This is the dividend of the Lunation Rule.
It may be difficult to fathom that such precise figures apparently are the results of calculations starting from the symbolic numbers associated with the amount of divination sticks prescribed by the Commentary on the Attached Words. Put in bare figures, the calculation is:
1 + 2 + 3 + 4 = 10
5 x 10 = 50
50 - 1 = 49
49 x 2 = 98
98 x 3 = 294
294 x 4 = 1,176
1,176 + 19 + 1 = 1,196
1,196 x 2 = 2,392
(2,392 / 81 = 29 43/81 = 29.5308642, the length of the Three Concordances Calendar's lunation, which deviates from the modern figure by 0.002763 day).
The last calculation is enclosed in parentheses because it does not occur in the History of the Han, which is content with finding the value of the Lunation Rule. The seemingly systematic and straightforward progression of the numbers 1-2-3-4 applied to both the addition and the multiplication in the preceding calculations is both fascinating and luring. But this is not how the Lunation Rule is calculated, on the contrary, the calculations take the Lunation Rule as their starting point. None of the other numbers, except for 19, the length of the Rule Cycle (zhang章) expresses any calendrical units, nor are they in any way relevant to calendrical computations. To reconcile numerology with the numbers of the calendar requires more numerology. The problem to be solved is how to bridge the gap between the number of the Lunation Rule of the calendar and the number of the Great Expansion of the Commentary on the Attached Words in the most simple and elegant way possible.
From the point of view of the author of the QZD, the purpose of the correlations between the numerology of the Book of Changes and the calendar computations may have been two-fold: On the one hand it endows the Book of Changes with a cosmic authority and, on the other, it constitutes an extension of the logical basis of the Book of Changes' capacity for predicting the future. When it is possible, by means of calculating the ends and beginnings of the various cycles, to tell which hexagram, line, phase, stem or branch is correlated to any day in the future, it is also possible, by knowing what circumstances, qualities, or portents are correlated with the hexagram, line, phase, stem or branch, to predict what may happen on the day in question. It was therefore pertinent to provide a clear picture of the correlations between the hexagrams and the relevant spatio-temporal concepts.
In Kong Yingda's孔颖达edition section 1.8 of the Commentary on the Attached Words begins with the passage describing how the divination sticks are manipulated to form a hexagram. The passage contains a reference to the intercalation of months, and in the remaining part of section 1.8 there is a further allusion to a connection between the numerology of the Book of Changes and the calendar:
Qian's乾divination sticks are 216, and Kun's坤divination sticks are 144. The total is 360 corresponding to the days of a year. The divination sticks of the two chapters [of the Zhou yi周易] are 11,520 corresponding to the number of the myriad things.
The Qian hexagram is here considered to have six yang lines of the value 9. A moving yang line of the value 9 requires that the remainder obtained in the divination procedure should be 36, i.e. 6 x 36 = 216. The same is true for the Kun hexagram, which is considered to have six lines of the value 6. This requires that the remainder obtained in the divination procedure is 24, i.e. 6 x 24 = 144.
The number 11,520 is the result of the calculation of the total of the remainders obtained in producing all 64 hexagrams. The total number of lines thus produced would be 6 x 64 = 384; of these 384 lines half are yin and half are yang. Assuming, as above, that the yang lines have the value 9, this means that each of the 192 yang lines in the Book of Changes left a remainder of 36 divination sticks, i.e. 36 x 192 = 6,912. Each of the 192 yin lines would leave a remainder of 24 divination sticks, i.e. 24 x 192 = 4,608. Added, the two figures result in 11,520 which supposedly corresponds to “the number of the myriad things,” literally, “the number of the ten thousand things.”
QZD refers to both the divination procedure and the association between the divination sticks and the number of days in a year while elaborating on the correspondences between divination and calendrical science:
In the calendar 365 1/4 days are considered to be one year. In the Changes (i.e. the Commentary on the Attached Words) 360 divination sticks are considered to correspond to the days of one year. These are the numbers of the pitch-pipes and the calendar. “In 5 years there are two intercalations, therefore twice [returning the remainder to] the space between the fingers and afterwards there is a hexagram.” This is to make correspondence between the numbers of the pitch-pipes and the calendar.
This passage reflects the different results that occur when comparing the methods of the calendar with that of the pitch-pipes. The calendar measures or calculates the solar year whereas the pitch-pipes are the means by which the lunations are recorded. The latter procedure is known as ‘waiting for the vital material forces' (hou qi候气). It was believed that a specific vital material force (qi) existed only in a limited period of time thus making it possible to record time by the changing of the vital material forces if only the change taking place could be observed. By carefully filling and adjusting a number of pitch-pipes with the finest ashes, it was thought that the ashes would be blown out when a particular vital material force was in tune, so to speak, with a particular pitch-pipe. When correctly tuned a set of pitch-pipes would ideally during the course of a year one by one give off its ashes. Zheng Xuan郑玄explains:
The calendar is used to calculate the seasons, and the pitch-pipes are used to wait for the vital material forces. When the vital material forces, which lead for 15 days making one revolution, and the pitch-pipes influence each other, there are 360 days. This roughly constitutes the end, but the calendar's number has a remainder of 1/4. This is irregular and not uniform, so an intercalary month is established [during] the four seasons to complete the mutual correspondence between years and the seasons.
Zhang Huiyan张惠言 (1761-1802) correctly remarks that 5 days still remain to be accounted for. The calendar Zheng Xuan refers to is probably the Quarter Remainder Calendar which, as the name suggests, calculates the length of a tropical year to 365 1/4 days. The pitch-pipes, on the other hand, by calculating the lunations, which according to Zheng Xuan each contains two revolutions of vital material forces, end up with 360 days, i.e. 24 periods of 15 days = 360 days. It is this lack of compatibility between the two systems the author of QZD addresses in the passage translated above. He seems to identify the pitch-pipe method with the numerology involving the divination sticks (at least, the two give the same result), and he also suggests that the solution to the incompatibility already was known to the author of the Commentary on the Attached Words because the text points to the question of intercalations. However, the Commentary on the Attached Words contains nothing more on the issue than the few lines translated above, and with these as his point of departure the author of QZD sets out to reconcile the systems of the Book of Changes and the pitch-pipes with the sophisticated calendrical computations of the Later Han dynasty:
The yang [lines'] numerical designation is nine, and the yin [lines'] numerical designation is six. As to the numerical designations of yin and yang, there are 192 for each. When these (i.e. yin and yang) are multiplied by the four seasons [the result is] eight and there is a cycle. [When further multiplied by four the result is] 32 and there is a great cycle. 384 lines equal 11,520 divination sticks. Therefore, the hexagrams correspond to the years, the lines correspond to the months, and the divination sticks correspond to the days.
“The number of the Great Expansion must be 50 [...] to complete the transformations and make the spirits move.” Thus, for the ten [stems of] the days there are the five notes, for the twelve periods of the day there are the six pitch-pipes, and for the 28 stars there are the seven lodges [of each of the four corners]. All these 50 are those that greatly open things and send them forth.
Therefore, the 64 hexagrams and the 384 lines are ready, each having that which is attached to it. So when yang intones, yin harmonizes, and when man acts, woman follows. The way of heaven rotates to the left, and the way of earth moves to the right. Two hexagrams have twelve lines and [they cover] a period of one year.
Like the Commentary on the Attached Words, QZD correlates the divination sticks with the days of the year but whereas the Commentary on the Attached Words says the divination sticks of Qian and Kun are like the 360 days of the year, QZD says that the total of 11,520 divination sticks are like the days of the year. QZD further says that the 384 lines are like the months and the 64 hexagrams are like the years, thus incorporating the entire composition of the Book of Changes in the correlations. The key to understanding this is given in the last sentence translated above, “Two hexagrams have twelve lines and [they cover] a period of one year,” and the enigmatic reference to a “great cycle” of 32 in the beginning of the passage.
Assuming two hexagrams cover a period of one year, the 64 hexagrams will cover a period of 32 years, presumably the so-called great cycle. The twelve lines of the two hexagrams covering a year correspond to the twelve months, and in 32 years the number of months will total 12 x 32 = 384. If the 11,520 divination sticks correspond to the number of days in 32 years, the number of days in one year is 11,520 divided by 32 = 360. Although these correlations are more coherent and appealing than those of the Commentary on the Attached Words, a figure such as 360 days in a year is still a far cry from the capacities of the calendar calculators of the day. So the author of QZD continues:
The First Calendar had no [specific] name. Calculating the first Era Cycle was called Jia yin甲寅. The Art of Calculating the Hexagrams that Govern the Year says: When constantly using the Year Star to record the years, 76 [years] are one Era Cycle, and 20 Era Cycles are one Obscuration Cycle. Then, the accumulated [years gone by] is set up [on the calculating board in units of] the Obscuration Cycle's number of years (i.e. 1,520 years) to which is added [those years] that has [already] entered the Era Cycle's number of years (i.e. 76), and this is divided by 32. The remainder that is less [than 32] is, beginning with Qian and Kun, counted by two hexagrams to obtain each year. The final counting rod, then, [indicates] the hexagrams that rule the year.
Then, set up [on the calculating board] one year's accumulated Day Rules and divide this [by] 29 43/81, the obtained unit is called a month, and the obtained accumulation is 12 7/19 months in one year.
Having introduced the Era and Obscuration Cycles of the Quarter Remainder Calendar, the author of QZD in the next paragraph proceeds to a calendrical computation involving concepts and figures associated with the Three Concordances Calendar. The aim of this calculation is to find the number of lunations in a solar year, which is a trivial operation of dividing the number of days in a solar year by the number of days in a lunation. The latter figure is given as 29 43/81, whereas the former is not disclosed. A simple multiplication, however, will reveal the figure of “one year's accumulated Day Rules,” the days of one lunation multiplied by the number of lunations in one year, i.e. 29 43/81 x 12 7/19 = 365 385/1539. These figures belong to the Three Concordances Calendar.
The next step is to make the calendrical computations compatible with the numerology of the Book of Changes by constructing an Epoch Cycle:
Multiplying this (i.e. 12 7/19 months) by 76 results in 940 accumulated months or 27,759 accumulated days. This is one Era Cycle. Multiplying this by 20 results in 1,520 accumulated years or 18,800 accumulated months or 555,180 accumulated days. This is one Obscuration Cycle. If one again sets up an Era Cycle and multiply this by 64, it results in 1,776,576 accumulated days. When further multiplied by 60, it results in 192 Obscuration Cycles or 3,840 Era Cycles or 291,840 years. Dividing this by 32 results in 9,120 cycles. This is called the hexagrams corresponding to the years. The result in accumulated months is 3,609,600 and of these 107,520 are intercalary. Dividing this by the 384 lines results in 9,400 cycles. This is called the lines corresponding to the months. The result in accumulated days is 106,594,560. Dividing this by the 11,520 divination sticks results in 9,253 cycles. This is called the divination sticks corresponding to the days, and the Changes is one great cycle, the pitch-pipes and the calendar attain each other in it.
These figures are very impressive, indeed, and on closer inspection it seems that this is exactly what they are meant to be. The author of QZD first introduces (his misconception of) the Era and Obscuration Cycles of the Quarter Remainder Calendar, after which he presents the exact figures for the lunation (29 43/81) and the number of lunations (12 7/19) of the solar year according to the Three Concordances Calendar. In the following calculations aiming at the construction of an epoch cycle, he turns back to the cycles of the Quarter Remainder Calendar while starting from the figure 12 7/19. This is probably also an attempt to demonstrate that the system of the Book of Changes about to be disclosed transcends even the calendars, which during the Han were changed several times, and thus to lay claim to greater continuity. This is, of course, possible only because while the two calendar systems differ as to the length of a lunation (29 43/81 as opposed to 29 499/940 days) and the length of a year (365 385/1539 as opposed to 365 1/4 days), the number of lunations of a year is the same.
To construct an epoch cycle, the author of QZD wants to find, as it were, the ‘common denominator' for the various cycles involved, so starting with an Era Cycle of 76 years, he first multiplies this by the 64 hexagrams and then by 60, which corresponds to a full cycle of the stems and branches. However, the sequence in which these multiplications are performed may obscure the fact that 76 multiplied by 60 (= 3 x 20) results in the Epoch Cycle of 4,560 years of the Quarter Remainder Calendar. This is subsequently multiplied by the number of hexagrams resulting in 64 Epoch Cycles or 291,840 years or 192 bushou蔀首, and by the end of this period the hexagrams, the lines, and the divination sticks have all returned to their starting point having completed the various numbers of cycles.
Unfortunately, QZD is corrupt where the figure is given for the number of cycles the 384 lines have passed through, and as mentioned above, Dong Youcheng (1791-1821) emended this to the figure 9,120 by leaving out the intercalary months. The figure 9,120 corresponds to the number of cycles the hexagrams pass through during the same time and is based on the assumption 1 year = 2 hexagrams = 12 lines. But the very motivation for the entire string of calculations is to include the intercalary months, to harmonize the pitch-pipes and the calendar, by constructing an epoch cycle within which the other cycles are contained, and by the end of which there is a concordance of phase, i.e. all the cycles have returned to the starting point. Thus in a period of 291,840 years, the hexagrams pass through 9,120 cycles (i.e. 291,840 / 32) and the lines pass through 9,400 cycles (i.e. 3,609,600 / 384). The reason why the lines pass through 280 more cycles is that while 32 hexagrams correspond to 384 lines, 32 years, according to the calendar, corresponds to 395 15/19 months, so for every cycle of 32 years, the cycle of the lines falls short by almost 12 months (11 15/19 to be precise). Therefore the lines must pass through an additional number of cycles, but after having completed 9,120 and 9,400 cycles, respectively, the hexagrams and the lines have returned to the starting point.
As to the divination sticks corresponding to the days, QZD clearly states (in spite of a minor error in the number of accumulated days) that the result is 9,253 cycles. This figure proves that the intercalary months are not to be disregarded as Dong Youcheng suggested. The number of accumulated days is 106,594,560, which divided by the number of years 291,840 results in 365 1/4, thus demonstrating that the original correspondence between the divination sticks and the days of a year, 11,520 divided by 32 = 360, has been improved to include the intercalary months. The divination sticks need not go through as many cycles as the lines because they only fall short by 168 days in 32 years as compared to the almost 12 months of the lines.
The 32-Year Hexagram Cycle
In order to provide a useful system for divination purposes it was necessary to have a clear picture of the distribution of the 64 hexagrams in relation to the 32-year cycle. The entire hexagram cycle as well as a few of the hexagram pairs are therefore envisioned in a circular arrangement. The positions of the hexagrams and the hexagram lines are explained in some detail in a passage following immediately after the paragraphs ending, “Two hexagrams have twelve lines and [they cover] a period of one year:”
Qian乾 (1) is yang and Kun坤 (2) is yin. They govern together while moving alternately. Qian's correct [position] is in the 11th month zi子 (i.e. branch no. 1), moving left. Yang's season [lasts for] six [months]. Kun's correct [position] is in the 6th month wei未 (i.e. branch no. 8), moving right. Yin's season [lasts for] six [months]. Assisting and following [each other] they complete the year, and when the year ends, the next follows in Zhun屯 (3) and Meng蒙 (4). When Zhun and Meng govern a year, Zhun is yang and its correct [position] is in the 12th month chou丑 (i.e. branch no. 2). Its lines move left, and by parting the seasons they govern six branches. Meng is yin and its correct [position] is in the 1st month yin (i.e. branch no. 3). Its lines move right, and they also part the seasons to govern six branches. When the year ends, they are followed by the next hexagrams. The yang hexagrams are considered in correct [positions] in their branches, and their lines move to the left, parting the branches and governing six branches. When the yin hexagrams are in similar positions to the yang hexagrams, they retreat one branch and these are considered their correct [positions]. The lines [of the yin hexagrams] move to the right, parting the branches and governing six branches. Only the hexagrams Tai 泰(11) and Pi否 (12) are both in correct [positions] in their branches. They are both alike in their branches and move left accompanying each other. Zhong fu中孚(61) is yang, and its correct [position] is in the 11th month zi子 (i.e. branch no. 1). Xiao guo不过 (62) is yin, and its correct [position] is in the 6th month wei未 (i.e. branch no. 8). They are modeled on Qian (1) and Kun (2). After a period of 32 years, there is a cycle, and the 64 hexagrams, the 384 lines, and the 11,520 divination sticks repeat [the cycle] following in the correct [positions].
|
|
|
|
|
 |
|
 |
|
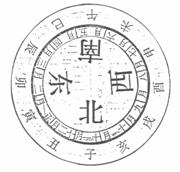
Plate1. Diagram of months, branches, Plate 2. Hui Dong's diagram of the 12 months, and the compass points hexagram lines, and branches
The following discussion of the actual positions and movements of lines and hexagrams should be viewed as occurring in a diagram of a circular arrangement of months and branches correlated with the compass points (see Plate 1). Starting with the movements of the hexagrams within the diagram, i.e. whether they move left or right, this has generated much confusion. The directions are explained by the commentary on the Consultation Charts (Ji lan tu稽览图, hereafter JLT): “East is left, west is right, south is in front, and north is behind.” As to the movements of Qian and Kun, Zhang Huiyan张惠言refers to Hui Dong's惠栋(1697-1758) Diagram of the Lines and Branches (Yao chen tu爻辰图), (see Plate 2) saying:
Qian is in the correct [position] in zi子 (branch no. 1) and moves left [from] zi [through] yin寅 (no. 3), chen辰 (no. 5), wu午(no. 7), shen申 (no. 9) [to] xu戌 (no. 11). Kun is in the correct [position] in wei未(no. 8) and moves right [from] wei未 [through] you酉(no. 10), hai亥(no. 12), chou丑 (no. 2), mao卯(no. 4) [to] si巳 (no. 6).
Although even a cursory glance at the diagram reveals that both Qian and Kun move clockwise through the branches, it may be argued that Qian, going from north towards east, moves left, while Kun, going from a southwestern point towards west, moves right. This only takes into account the initial movements of the hexagrams, however, and describes only a quarter of their orbits. When, for example, Qian moves on from east towards south, is it still moving left? If, on the other hand, the clockwise movement through branches nos. 3, 5, 7, 9, and 11 is described as moving left, then, taking a less narrow view, the clockwise movement by Kun from branch no. 8 through 10, 12, 2, 4, and 6 cannot logically be described as moving right. Zhang Huiyan张惠言sums up some of the confusion as to what is left and what is right with regard to the diagram:
[Hui Dong惠栋] introduces the order of the mutual production of the 12 pitch-pipes of the Rituals of the Zhou Dynasty with Zheng [Xuan's]郑玄 commentary as evidence for this. He says that Master Zhu [Zhen's朱震, 1072-1138] exposition of the diagram, [which has the counter-clockwise sequence] wei未(no. 8), si巳(no. 6), mao卯(no. 4), chou丑(no. 2), hai亥(no. 12) you酉(no. 10) to be moving right, is wrong. Now, I say this is not the case. When the book (i.e. QZD) says of Tai泰and Pi否, “They are both alike in their branches and move left accompanying each other,” then it may be inferred that the remaining hexagrams are said to move left and right without following each other. Hui [Dong] says, that Kun is in the correct [position] in wei未(no. 8). If [moving counter-clockwise] from si巳(no. 6) towards mao卯(no. 4) is moving left, how can Pi, being in the correct [position] in shen申(no. 9) and [moving clockwise] from you酉(no. 10) towards xu戌(no. 11) be considered moving left? Meng蒙 is in the correct [position] in yin寅 (no. 3). If, as in Hui [Dong's] usage, it should [move clockwise] from chen辰 (no. 5) towards xu戌(no. 11), how can this be considered moving right? In all the talk of left and right everyone just speaks according to his own position. As to the positions of the twelve pitch-pipes, “when Qian and Kun are united together, they are all produced.” Moreover, “three to heaven and two to earth” of the Changes [refers to] the positions of the six lines. Therefore, alternating and accompanying each other is not necessarily the same as this. The Eight Trigrams and the six positions of the Fire Pearl Forest火珠林 [have] Qian in zi子(1), yin寅 (3), chen辰(5), wu午 (7), shen申(9), xu戌 (11), and Kun in wei未 (8), si巳 (6), mao卯 (4), chou丑(2), hai亥(12), you酉 (10). It is based on this.
Thus the movements and positions of the hexagrams are conceived of as projections on to a cosmic diagram and not on to the cosmos itself. JLT's interpretation of the directions suggests an orientation towards the south, which means that moving to the left is moving from west to east. If, for example, Qian was understood as some kind of imaginary projection on the firmament, an observer would be facing south, keeping his back to the north, and expect Qian to move from west through south to east or, in terms of branches, from shen申(9) through wu午(7) to chen辰(5), i.e. counter-clockwise. This is not the case, however, because the diviner only pictures the movements and positions as occurring on a diagram which he can keep in front of himself, and therefore it is equally possible for Qian to move from west to east through north. Consequently, moving left means moving clockwise and moving right means moving counter-clockwise as in Zhang Huiyan's张惠言 Diagram of Two Hexagrams Parting Time to Rule Six Branches (Er gua jian shi er zhi liu chen tu二卦间时而治六辰图) (see Plate 3).
In spite of Zhang Huiyan's argumentation, which may be based on Song scholarship represented by Zhu Zhen朱震(1072-1138), it seems modern Chinese research on the subject has failed to see the significance of this. For example, Fung Yu-lan's冯友兰explanation is identical with Hui Dong's, as are all the articles, diagrams, and tabulations in The Great Encyclopedia of Yi Studies, Yi xue da cidian易学大辞典. The same explanation is found in another encyclopedic work, The Encyclopedia of the Changes of Zhou, Zhou yi cidian周易辞典, as well as in new comprehensive studies by leading Chinese Yi jing scholars such as Liao Mingchun廖名春(b. 1956) and Xu Qinting徐芹庭 (20th cent.). These scholars may feel on safe ground, though, as their interpretations are based on the explanations given by Zheng Xuan郑玄 (127-200) and Wei Zhao韦昭 (d. 273), who are both well-versed in the philosophy and cosmology of the Later Han.
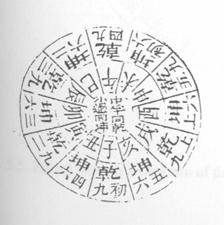
Plate 3. Diagram of Qian and Kun
Additional evidence for Zhu Zhen's朱震 and Zhang Huiyan's张惠言 interpretation can, however, be adduced from QZD itself, namely, the statement, “When the yin hexagrams are in similar positions as the yang hexagrams, they retreat one branch ...”. The commentary on this passage states: “The yin hexagrams and the yang hexagrams having similar positions means that if they in similar months are positioned opposite each other, it is the yin hexagrams that retreat one branch.” Zhang Huiyan quotes Dong Youcheng who gives an example of how this works: “Qian is in zi子(no. 1) and Kun is in wu午(no. 7) but as wu is opposite zi, Kun retreats to a correct [position] in wei未 (no. 8).” Now, Zhang Huiyan said, Kun moves counter-clockwise, i.e. towards the right, so when Kun retreats, it should be in the opposite direction, and this is exactly what the movement from wu (no. 7) to wei (no. 8) is. If Kun moves clockwise, as argued by Fung Yu-lan冯友兰 et al., the movement from wu (no. 7) to wei (no. 8) could never be construed as retreating.
The only exception to the rule of alternating and retreating are the hexagrams Tai (11) and Pi (12), and the commentary explains:
That only Tai and Pi are both in correct [positions] in their branches means that the hexagram sequence is not applied. [According to the hexagram sequence] the Tai hexagram should be in the correct [position] in xu戌 (no. 11) and Pi should be in the correct [position] in hai亥(no. 12). Xu is the location of Qian's substance, and hai is the month when Kun is waxing and waning. Tai and Pi [have both] Qian and Kun [trigrams], so the substance and the qi become mutually disordered by them (i.e. the branches xu and hai), and therefore [Tai and Pi] avoid them and are both in correct [positions] in their branches. This means Tai is in the correct [position] in the first month, and Pi is in the correct [position] in the seventh month. The six lines are all either Tai obtaining the Qian [trigram] of Pi or Pi obtaining the Kun [trigram] of Tai. These branches move to the left, which means that [the positions of] Tai from the first month to the sixth month are all yang lines, and [the positions of] Pi from the seventh month to the twelfth month are all yin lines. As to Tai and Pi, each one follows the other.
As Zhang Huiyan points out, the commentary is mistaken about the positions of the yin and the yang lines. The yang lines occur from the tenth to the third month, and the yin lines occur from the fourth to the ninth month, as in Zhang Huiyan's Diagram of Tai and Pi Both Being in the Correct [Positions] in Their Branches and Moving Left Following Each Other (Pi Tai ge zhen qi chen zuo xing xiang sui tu否泰各贞其辰左行相随图) (see Plate 4).
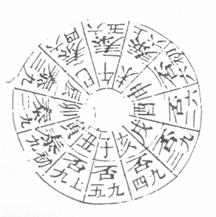
Plate 4. Diagram of Tai and Pi
The 32-year cycle of the 64 hexagrams starts with Qian乾 and Kun坤, which are said to be in their correct positions in the branches corresponding to the 11th and 6th months, respectively. It is further said that the hexagrams Zhong fu中孚 (61) and Xiao guo小过 (62) are modeled on Qian乾 and Kun坤, and that the yin hexagrams retreat if they are in similar positions to the yang hexagrams. When the first year has gone, Qian and Kun are followed by Zhun屯 (3) and Meng蒙 (4), which are in their correct positions in the 12th and 1st months. From this it may be inferred that the 3rd year has Xu需 (5) and Song讼 (6) in the 2nd and 3rd months, and the 4th year has Shi师 (7) and Bi比 (8) in the 4th and 5th months. In the 5th year Xiao xu小畜 (9) and Lu履 (10), skipping the 6th month because that is already occupied by Kun, are in their correct positions in the 7th and 8th months. The 6th year is ruled by Tai (11) and Pi (12), which should logically be in the 9th and 10th months, but for the reasons explained above, they are in the 1st and 7th months instead. This introduces some disorder in the sequence, but the general idea seems to be that the hexagrams occur in the same sequence as in the received edition of the Book of Changes.
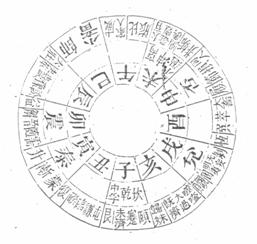Zhang Huiyan张惠言 also has a Diagram of the Sixty-four Hexagrams' Correct Branches (Liushisi gua zhen chen tu六十四卦贞辰图) (see Plate 5), but he does not explain the principles behind it. The positions and correlations of the hexagrams mentioned by QZD check out, whereas the results of the above attempt to reconstruct a sequence based on this information do not. Underneath the apparent lack of method of distribution, which allocates only two hexagrams to the branch si巳 (no. 6) and 10 hexagrams to wei未 (no. 8), a certain order may be observed. For example, when considered in relation to the compass points, the diagram divides into four groups with three branches and 16 hexagrams in each.
Plate 5. Zhang Huiyan's diagram of the 64 hexagrams
Elsewhere in QZD an occasional reference to a correlation between a hexagram and a month occurs; thus it is said that Tai泰 (11) is the hexagram of the 1st month, Yi益(42) is also said to be the hexagram of the 1st month, Sheng 升(46) is said to be the hexagram of the 12th month, and Gui mei归妹(54) the hexagram of the 8th month. When these correlations are checked with Zhang Huiyan's diagram, it is only Tai that fits in. If, however, these correlations are checked with the tabulation of hexagrams and months found in JLT, it is only Gui mei that does not fit (it should be in the 9th month). The system of JLT correlates 60 hexagrams to the twelve months, which results in an even distribution of five hexagrams per month (see Plate 6). The remaining four hexagrams, Kan坎(29), Li离(30), Zhen震(51), and Dui兑(58), are the ‘pure hexagrams' (chun gua纯卦), which are composed of identical trigrams, and in this case, the trigrams that represent the four compass points in the arrangement of the so-called Diagram of Later Heaven (Hou tian tu后天图). The 24 lines of these four hexagrams are correlated to the 24 solar periods.
|
|
 |
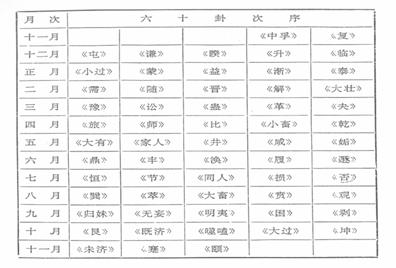Plate 6. JLT's correlation between the 12 months and the 64 hexagrams
It can be demonstrated that the 32-year cycle of QZD is based on JLT's tabulation of the correlations between the 60 hexagrams and the twelve months. Returning to Zhang Huiyan's diagram, it is divided into three concentric rings, the innermost of which contains the names of the twelve branches corresponding to the twelve months (see Plate 7). The middle ring, which has six empty places, contains the names of the following ten hexagrams: Qian乾(1), Kun坤(2), Tai泰(11), Pi否(12), Kan坎(29), Li离(30), Zhen震(51), Dui兑(58), Zhong fu中孚(61), and Xiao guo小过(62). The outer ring contains the remaining 54 hexagrams, and the hexagrams belonging to a particular branch are divided into two groups by a short vertical line, for example in branch no. 1, zi, the hexagram Gen (52) is separated from the three other hexagrams. Within each branch, those hexagram names that appear on the left side of the short vertical line belong to the hexagrams that retreat one place, i.e. they are yin hexagrams that originally would have been in a similar position to the yang hexagram. It may therefore be assumed that these yin hexagrams share certain features that will lead to a definition of that term as well as to a clear understanding of what ‘similar positions' (tong wei同位) means.
There are various conflicting ways to determine whether a hexagram is yin or yang, but the only thing the 14 hexagrams that are set apart in Zhang Huiyan's diagram have in common is that they occur as the second of a pair in the Book of Changes. It may therefore be assumed that the yang hexagram is the first of a pair (like Qian, the quintessential yang hexagram), and the yin hexagram is the second (like Kun, the quintessential yin hexagram). In Zhang Qicheng's (20th cent.) diagram (see Plate 7), the hexagrams Da you (14) and Xun (57) have been added to this group for the following reasons:
Furthermore, Dui 兑(58) being correct in the xu戌(branch no. 11) month is a mistake; it should be correct in you酉(no. 10). Xun巽(57) is correct in the you month, and it retreats one place, so it should be moved inside the xu month below the hexagram Bi贲(22). Da you大有(14) should be correct in the wei未(no. 8) month and placed before Gou姤 (44).
Plate 7. Zhang Qicheng's diagram of the 64 hexagrams
While Da you 大有(14) fits the description of a yin hexagram given here, Zhang Qicheng's张其成 rearrangement, as it appears in his diagram, merely amounts to changing its place within the three hexagrams positioned to the right of the vertical line. As I shall demonstrate below, it is correct that Da you should be placed before Gou, which can only mean to the left of the vertical line, so this must be another mistake in the diagram. Grouping Xun 巽(57) with the yin hexagrams, on the other hand, upsets the entire system, because Xun, being the first hexagram of the pair Xun 巽and Dui兑, is a yang hexagram. Apparently Zhang Qicheng finds it necessary to redefine the nature of Xun and have it retreat from branch no. 10 to no. 11 because he wants to place Dui 兑(58) in branch no. 10, which corresponds to due west, the position of the trigram Dui in the arrangement of the Diagram of Later Heaven. Zhang Qicheng does not state his reasons for rearranging the position of Dui, but if the motivation indeed is to integrate the compass points according to the Diagram of Later Heaven, Zhang Qicheng would also be compelled to move Li 离(30) from branch no. 8 to no. 7, corresponding to due south. That would not work, however, because it places Li (30) directly opposite its yang trigram, Kan 坎(29), which is in branch no. 1, corresponding to due north.
Comparing Zhang Huiyan's and Zhang Qicheng's diagrams of the 32-year cycle of QZD with the JLT tabulation of the correlations between the months and the hexagrams (see Plate 6) clearly shows that the former is based on the latter. Starting in branch no. 1, zi, in the circular arrangement, the name of hexagram Gen (52) appears to the left of the vertical line in the outer ring, indicating that it is a yin hexagram which has retreated one place, i.e. it has moved one place clockwise through the branches. This means it should have been correct in branch no. 12, hai, corresponding to the 10th month, and this is exactly the position of Gen in the JLT arrangement. Moving on to branch no. 2, chou, in the QZD diagram, the name of the hexagram Fu (24) appears to the left of the vertical line, indicating that it has retreated from branch no. 1, zi, corresponding to the 11th month, which is the position of Fu in the Ji lan tu稽览图tabulation. In the same way the remaining 12 yin hexagrams of Zhang Huiyan's diagram can be traced to their correct positions according to the JLT correlations. In the case of Da you (14), which in the QZD diagram occurs in branch no. 8, wei, its position in the JLT arrangement as correct in branch no. 7, wu, confirms the reclassification as a yin hexagram retreating by Zhang Qicheng.
The hexagrams placed to the right of the vertical lines on the outer ring in Zhang Huiyan's diagram are without exception in the exact same branches and months in the Ji lan tu. For example, in branch no. 1, zi, in the 32-year cycle the three hexagrams Yi (27), Jian (39), and Wei ji (64) occur, and this is also the position of the three hexagrams in the JLT arrangement. As to the ten hexagrams in the middle ring of Zhang Huiyan's diagram, there are some irregularities. The four hexagrams Kan (29), Li (30), Zhen (51), and Dui (58), of course, do not occur in the JLT tabulation. Tai (11) and Pi (12), which are in branches nos. 3, yin, and 9, shen, respectively, also occur in these branches in JLT. The pair Zhong fu (61) and Xiao guo (62), which according to QZD is modelled on Qian and Kun, are in the branches nos. 1, zi, and 8, wei, in Zhang Huiyan's diagram, but in JLT only Zhong fu is in the same branch, while Xiao guo is in branch no. 3, yin, instead. Finally, Qian and Kun, which in Zhang Huiyan's diagram also are in branch nos. 1 and 8, are in the branch nos. 6 and 10 in JLT. It is thus clear that the two systems differ only in a few cases where QZD has exact directions as to the positions whereas when precise information is lacking, Zhang Huiyan's diagram is based on the correlations of JLT. Whether or not this was the intention of the author of QZD will remain undecided.
Zhang Huiyan's diagram does not shed any light on the meaning of ‘similar positions'. The QZD commentary clearly says that ‘similar positions' means ‘positioned crosswise' but there is only one example of that among the 15 cases where the yin hexagram retreats one position: The hexagram Sun (41) is in branch no. 7, wu, and Yi (42) is in no. 1, zi, therefore Yi retreats one position to branch no. 2, chou. It seems that when whoever constructed Zhang Huiyan's diagram, copying the correlations of JLT, encountered a pair of hexagrams, which are both correlated to even or to odd branches, he would move the second hexagram of the pair one branch in a clockwise direction. This could not only be interpreted as the yin hexagram retreating, but would also facilitate the alternation of the hexagrams as prescribed by QZD.
The correlations between the hexagrams and the months and branches, as these appear in Zhang Huiyan's diagram, are thus for the greater part not based on QZD but on JLT. It is therefore in the latter work that the rationale behind these correlations should be sought. Fung Yu-lan has described the system, which allocates five hexagrams to each month or branch. Each of the five hexagrams correlated to a particular month is given a title: One is called Great Officer (Da fudd f大夫), one is called Minister (Qing卿), one is called Duke (Gong公), one is called Feudal Prince (Zhu hou诸侯), and one is called Son of Heaven (Tian zi天子). As Fung Yu-lan demonstrates, the 12 hexagrams bearing the title Son of Heaven symbolize the fluctuation of yin and yang during the course of a year starting in branch no. 1:
The organization of the rest of the hexagrams as well as their correlations to titles, months, and branches lacks a corresponding systematization.
Thus, having presented how the 32-year cycle of QZD was pictured by later scholars—basing themselves on the sparse information of the text—as an arrangement that would fit in a diagram, it is necessary again to turn to JLT to get an idea of the actual application of the hexagrams to divination. It will soon become apparent, however, that the author of QZD shares the assumptions and ideas expressed in JLT although the latter relates them to a different 32-year cycle of hexagrams. In fact, JLT has several examples of schemes that correlates the hexagrams with months and branches, but taking a prominent position among them is a tabulation of hexagrams in pairs forming a veritable divination manual complete with all the figures needed to apply the hexagrams to predictions of future events. The first two entries of this divination manual goes:
1. Qian. The generation line is in xu戌(no. 11), and the first line is in zi子(no. 1).
Kun. The generation line is in you (no. 10), and the first line is in wei未(no. 8).
The two [hexagrams'] combined divination sticks are 360.
Divided for each, Qian has 216, and Kun has 144.
The course of the lineage of the two [hexagrams'] combined is 1,440.
Divided for each, Qian has 768, and Kun has 672.
2. Zhun. The generation line is in yin (no. 3), and the first line is in yin.
Meng. The generation line is in xu (no. 11), and the first line is in si (no. 6).
The two [hexagrams'] combined divination sticks are 336.
Divided for each, Zhun has 168, and Meng has 168.
The course of the lineage of the two [hexagrams'] combined is 1,408.
Divided for each, Zhun has 704, and Meng has 704.
Although the correlations between the branches and the hexagrams in this tabulation are different from those of the 32-year cycle of QZD, the two cycles seem to have been used in the same manner. At least, the author of QZD is also familiar with the figures referred to as the ‘courses of the lineage' and attempts to explain the concept:
Confucius said: He who considered 760 [years] to be the generations' course of the lineage was Yao. Obtaining heaven's origin by means of the jia zi甲子is the art of inference. The one who considered the reversal of 6 and 8 and 9 and 7 to be the generations' course of the lineage was King Wen. Reckoning the hexagram lines' four [designations] is the art of numbers.
Zheng Xuan explains in greater detail in the commentary:
The jia zi constitute an Era Cycle, starting on the first day of the 11th month. Each Era Cycle is 76 years. Thus, the generations accumulate 1,520 years after which they start over again. If so, then a period of 76 years. Early in the morning on the first jia zi day of the 11th month. Yao already considered this to be one yin and one yang, so he divided it in the middle. This inference/deduction is regarded as the course of the lineage system.
In the Changes there are four images, and King Wen used them in his [art]. He arranged 6 in the north to represent water, he arranged 8 in the east to represent wood, he arranged 9 in the west to represent metal, and he arranged 7 in the south to represent fire. Thus he makes it complete providing one hexagram line and adjusting the four operations. From this, then, the numbers 4 x 8, 4 x 9, 4 x 7, and 4 x 6 are produced. As to the lines, if doubling them, every hexagram on average obtains 720 years. The talk of reversal (lit. going and coming) means that outside (i.e. above average) are the yang [figures] and inside (i.e. below average) are the yin [figures].
The author of QZD further states:
As to the method [of calculating the time of] a course of a lineage enjoying the state, the yang [principle] is enthroned by means of 9 and 7. 9 and 7 means 4 x 9 and 4 x 7. The yin [principle] is enthroned by means of 6 and 8. 6 and 8 means 4 x 6 and 4 x 8. When the yang [principle] loses the throne, it is 36, and when the yin [principle] loses the throne, it is 24.
And Zheng Xuan explains:
4 x 9 are 36, 4 x 7 are 28, and the total is 64. 4 x 6 are 24, 4 x 8 are 32, and the total is 56. This is King Wen reckoning the hexagram lines to be one generation. Altogether it is 720 years. As to the years and the course of the lineage, these are the number of years on the throne. When enthroned, the [values] of the static and the changing [hexagram lines] are simply combined, and for the virtuous, they are doubled, therefore the course of the lineage is 720.
JLT spells it out most explicitly in the paragraph preceding the tabulation of the 32 hexagram pairs of the divination manual:
The Art of the Sixty-four Hexagrams says: The yang line is 9, and the yin line is 6. The Art of the Course of a Lineage says: The yang line is 9 and 7, and the yin line is 8 and 6. If the six positions of Qian had old yang lines of [value] 9, then multiplying 36 by the 6 lines results in 216; [if the six positions] had young yang lines of [value] 7, then multiplying 28 by the 6 lines results in 168. Adding the above two figures results in 384. Doubling this gives 768. If the six positions of Kun had old yin lines of [value] 6, then multiplying 24 by the 6 lines results in 144; [if the six positions] had young yin lines of [value] 8, the multiplying 32 by the 6 lines results in 192. Adding the above two figures results in 336. Doubling this gives 672. The two courses of a lineage numbers of Qian and Kun, added, are 1,440. All the yang lines take 64 as the rule, this is multiplied, and the result is doubled. All yin lines take 56 as the rule, this is multiplied, the resulting figure of which is doubled.
From the above it is clear that the reign of the lineage is calculated on basis of the numerical designations of the hexagram lines and the number of divination sticks that lead to these designations. The method of obtaining the reign of the lineage associated with a certain hexagram may be expressed in a formula where A is the number of yin lines of the hexagram and B is the number of yang lines:
2 x [A x (4 x 6 + 4 x 8) + B x (4 x 7 + 4 x 9)]
For example, in the case of the hexagram Fu (24), the calculation is:
2 x [5 x (4 x 6 + 4 x 8) + 1 x (4 x 7 + 4 x 9)] = 688
In the extreme cases of hexagrams Qian and Kun, which are composed entirely of yang or yin lines, half of the calculation within the brackets is dropped. For example, in the case Qian:
2 x [6 x (4 x 7 + 4 x 9)] = 768
Leaving aside Qian and Kun, the combinations of yin and yang lines of the remaining hexagrams make the following course of the lineage numbers possible: 688, 704, 720, 736, and 752. To apply these figures to a dynasty, it is necessary to determine which hexagram ruled the year when the dynasty was founded. This operation, which amounts to freezing the 32-year cycle of the hexagrams at a fixed point in time, requires a starting point, and this is where the concordance cycle is indispensable. As stated above, if the beginning of the largest cycle can be ascertained, “the state of any of the smaller cycles, which by definition began at the same time, could be determined ...” The paragraph on The Art of Obtaining the Hexagrams that Govern the Year from QZD translated earlier, is an example of how to do this calculation:
The First Calendar had no [specific] name. Calculating the first Era Cycle was called Jia yin甲寅. The Art of Calculating the Hexagrams that Govern the Year says: When constantly using Jupiter to record the years, 76 [years] are one Era Cycle, and 20 Era Cycles are one Obscuration Cycle. Then, the accumulated [years gone by] is set up [on the calculating board in units of] the Obscuration Cycle's number of years (i.e. 1,520 years) to which is added [those years] that has [already] entered the Era Cycle's number of years (i.e. 76), and this is divided by 32. The remainder that is less [than 32] is, beginning with Qian and Kun, counted by two hexagrams to obtain each year. The final counting rod, then, [indicates] the hexagrams that rule the year.
The only really weak point in this scheme reveals itself when it comes to calculating the beginning of the largest cycle or, in other words, the first year, i.e. the number of years that have passed from the origin of heaven to a known point in time. This figure could not be based on astronomical or calendrical computations, rather it was the result of what Sivin calls ‘literary numerology,' i.e. it was decided by the authors of the Apocrypha. In two Apocrypha belonging to The Springs and Autumns (Chunqiu春秋), The Order of the Charge and the Calendar (Ming li xu命历序) and The Inclusion of the Original Charge (Yuan ming bao元命包), it was settled that the known point in time should be 481 BCE, the year the mythical beast, the qilin麒麟, was captured, an event that signalled the end of the Springs and Autumns period and foreboded the death of Confucius. The authors of the Apocrypha decided that in the year 481 BCE, 2,760,000 years had elapsed since the creation of the world, and this is copied into the chapter on pitch-pipes and calendars of Hou han shu, which also cites QZD as a source.
Having formulated this time span, or during the process of doing so, it became necessary to relate the figure to the calendrical computations. In the case of QZD, which operates with King Wen's reception of the Mandate as the fixed point in time and a time span of 2,759,280 years, the concordance cycle as calculated above corresponds to 64 Epoch Cycles (yuan元). It was also demonstrated above that the numerology of QZD is based on the constants of the Quarter Remainder Calendar, which has an Epoch Cycle of 4,560 years, thus the concordance cycle or ‘the Great Year' is 4,560 years multiplied by 64, resulting in 291,840 years. One Epoch Cycle corresponds roughly to 380 revolutions of Jupiter, so astronomical computations showed that an Epoch Cycle had begun in 1681 BCE, and that the next would begin in 2879 CE. For example, if the years from 481 BCE to 2879 CE are added to the fictitious 2,760,000 years, the result is 2,763,360, which divided by the number of years of the Epoch Cycle results in 606. Consequently, the year 481 BCE is set somewhere in the 606th Epoch Cycle. Once this has been established, it is a matter of trivial arithmetic to find out which hexagram pair rules a certain year.
For example, the 2,759,280 years of QZD is divided by the the number of years of the concordance cycle, which results in 9 concordance cycles and a remainder of 132,720 years. The remainder is divided by the number of hexagrams of the hexagram cycle, 32, which results in 4,147 hexagram cycles and a remainder of 16 years. The remainder is counted through from the pair number one, Qian-Kun, which rules the first year, number two, Zhun-Meng, which rules the second, and so on until the pair which rules the 16th year is arrived at: Xian (31) and Heng (32). By looking up in the divination manual, or calculating it himself, the diviner can now determine the course of the lineage associated with the year 1201 BCE when King Wen supposedly received the Mandate. For both hexagrams the number is 720, and the figures discussed earlier seem to suggest that the hexagram that actually ruled the month of the enthronement should be pinpointed, thus making the course of the lineage 720, but QZD is not clear on this point. In fact, the information in QZD on the actual application of the 32-year cycle is rather sparse whereas JLT, mostly due to later interpolations and appended commentaries, abound with examples some of which are as late as 820 CE. I shall here limit myself to an example, for which there is also support in QZD, of a more refined use of the hexagram cycle involving the course of the lineage as well as the stems and the branches.
The Epoch Cycle of the Quarter Remainder Calendar is analysed in QZD as composed of three Obscuration Cycles (bushou蔀首) and one Obscuration Cycle is composed of 20 Era Cycles. This, in effect, means that the Epoch Cycle is composed of 60 Era Cycles, which makes the Epoch Cycle compatible with a cycle of the stems and branches. Thus to find the stem and branch for a particular year, it is only necessary to divide the 2,759,280 years by the number of years in an Epoch Cycle, which, of course, results in 605 Epoch Cycles (cf. above) and a remainder of 480 years. The remainder is divided by the number of years of the Era Cycle, which is 76, resulting in 6 Era Cycles and a remainder of 24 years. Because there is concordance of phase between the Era Cycles, the stems and branches, and the Epoch Cycles, every time the latter begins a new cycle, the first year of the first Era Cycle of the 480 years is a jia zi甲子 (stem no.1/branch no. 1) year. The first year of the second Era Cycle is a geng chen庚辰 (no. 7/no. 5) year, the first year of the third Era Cycle a bing shen丙申 (no. 3/no. 9), and so on. Thus following the sexegenary cycle counting through the Era Cycles, the last year of the remainder of 24, which corresponds to the year 1201 BCE, is a bing xu丙戌 (no. 3/no. 11) year.
Having determined the stem and branch of any particular year in question as well as the hexagram pair that rules the year in which the dynasty was founded, and thus the reign of the lineage number, the diviner can proceed. If, for example, the divination is concerned with forecasting the events of the 52nd year of the dynasty, the reign of lineage number is divided by 52, and the remainder is counted through by the sexegenary cycle to find the stem and branch in question. Actually, it is only the stem that is of any interest in the last operation, because the ten stems are correlated to various, mostly tragic, events, that have played significant roles in Chinese history: Jia甲 (no. 1) and yi乙 (no. 2) signified famine, bing丙 (no. 3) and ding丁 (no. 4) drought, wu戊 (no. 5) and ji己 (no. 6) resurgence, geng庚(no. 7) and xin辛(no. 8) war, and ren壬(no. 9) and gui癸(no. 10) floods. Thus the stem arrived at indicates which of the these events may be expected for the year under consideration.
Commentaries attached to JLT show that this divination was practiced frequently during the period of disunity in the centuries following the collapse of the Han dynasty. I have searched for Han dynasty examples of this kind of divination. In the wake of Wang Mang's downfall and death in 23 CE, at least a dozen contenders in the struggle for power emerged, half of them belonging to the house of Han. Various prognostications played an important part in what has been described as a psychological warfare between the parties. The histories of the Han has preserved several accounts of the ideological debate between Gongsun Shu公孙述(d. 36), who ruled the area that roughly corresponds to present day Sichuan, and Liu Xiu刘秀, who became known to posterity as emperor Guangwu光武. A well-known example says that Gongsun had a dream in which a man told him that the number twelve is the limit. This was interpreted by his diviners to mean that after twelve rulers, the house of Han had reached its limit, and if Empress Lü of the Former Han was included in the count, Guangwu would be number 13, so the time had come for Gongsun Shu to take over. Diviners of Guangwu's camp turned the dream against Gongsun himself, saying that after 12 years Gongsun had reached the limit—he had proclaimed himself king in 24 and he was, in fact, killed in 36.
The Huayang guozhi华阳国志—compiled in the 4th century by Chang Qu常璩—informs us that emperor Guangwu in the course of this debate conceded that the house of Han would perish after 920 years. It is clear, I think, that prior to such a statement one or more diviners or prognostication texts had been consulted. I suggest that—if it is not QZD that was consulted in this connection—it is a text or a person with knowledge of the divination system described above. As mentioned previously, the Later Han was founded in 25 CE, but it was only the following year (26 CE) that it was decided to adopt the phase symbolized by the element fire. So if Guangwu were to avail himself of QZD's divination system to predict the duration of the house of Han, he should start by finding the pair of hexagrams that rules the year 26 CE. However, the house of Han had by 26 CE already been in possession of the Mandate for more than two centuries, and because Wang Mang's dynasty was considered an interregnum, the Han reign had not been discontinued. The Huayang guozhi says the foundation of the Han happened in an yi wei乙未year, when Liu Bang assumed the title of King, i.e. in 206 BCE. So if we are to calculate how long the Han had possessed the Mandate by 26 CE, we should count from 206 BCE, and the result is 232 years. If we subtract these 232 years from the 920 years mentioned by Guangwu, the result is 688 years. This is one of only 9 possible outcomes of QZD's divination system and it is obtainable by only three different pairs of hexagrams—those containing five yin lines and one yang line. Suppose pair no. 8 of the 32-year cycle governed the year 26 CE, the prediction would be that the ruling house would last for 688 years. So by adding the 232 years already gone by, emperor Guangwu would be right in saying the Han will perish after 920 years if his prognostication said 688 years. Furthermore, counting backwards reveals, that when Liu Bang originally founded the dynasty, it was right at the beginning of the 32-year cycle in a year governed by Qian and Kun, the quintessence of yang and yin. Surely, this cannot but be construed as an auspicious sign.
There is, of course, no certain way to verify this theory but I have an example which may serve as circumstantial evidence. QZD states that from the beginning of time—the origin of heaven—until the venerable king Wen received heaven's mandate in approval of his conquest of the Shang dynasty and the foundation of the Zhou, 2,759,280 years have elapsed. In order to figure out which pair of hexagrams ruled the year king Wen founded the Zhou this figure should be divided by 32 which results in 86,227½ 32-year cycles. Half a cycle indicates that pair no. 16 ruled the year in question. Pair no. 16 consists of the hexagrams Xian咸and Heng恒, which are both composed of three broken and three solid lines. According to the formula described earlier, pair no. 16 indicates a reign of 720 years. Disregarding all historical facts, and assuming that when the 720 years of Zhou reign came to an end, the Han dynasty was founded, because in the minds of the Later Han cosmologists, the Han was the legitimate successor to the Zhou. This, of course, means that—like Wang Mang's dynasty—the Qin dynasty is considered an interregnum. From this it follows, that the Zhou dynasty was founded in 926 BCE, and that this year was ruled by hexagram pair no. 16 of the 32-year cycle. Above it was established by counting backwards from 26 CE to 206 BCE that the latter year—the foundation of the house of Han—was ruled by hexagram pair no. 1. Now, counting forward from 926 BCE should hopefully give the same result, which it does. 720 divided by 32 is 22½, and starting in 926 which is a Xian-Heng year, the first Qian-Kun year we encounter is 910, the next Qian-Kun year is 894, the next 878, and so on down to 238 BCE, and finally 206 BCE, the year Liu Bang proclaimed himself king of the Han.
